Northern Renaissance Instruments
6 Needham Avenue, Chorlton-cum-Hardy, Manchester M21 8AA, U.K.
phone & fax. +44 (0) 161 881 8134 ; proprietor: Dr. Ephraim Segerman [USA]
e-mail: post@nrinst.co.uk ; on internet: http://www.nrinst.co.uk
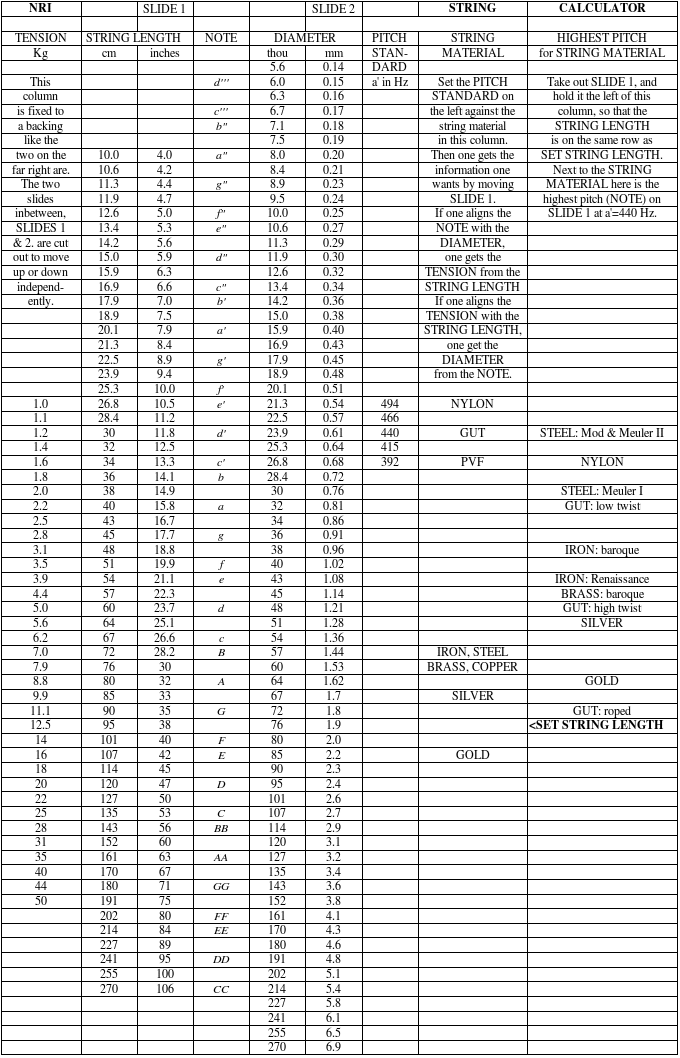
STRING CALCULATOR
The String Calculator is a device that works like the slide rules that were universally used for calculating before electronic calculators became available. It relates the string diameter (or equivalent diameter if the string is wound or twisted), the string stop (otherwise called the vibrating string length), the fundamental vibration frequency (which is a combination of the nominal pitch and the pitch standard) and the density of the string material (which is that of the core in a wound string). With the String Calculator, if we know or can estimate all of the other factors, we can find the remaining one. In addition, the Calculator allows the estimation of the highest pitch that a string can safely be tuned to.
Stationary parts of the calculator are the left-most column, which shows the tension, and the two right-most columns which are concerned with the string material, the left of which represents the density, and the right of which represents the strength. The rest of the Calculator is composed of two Slides. The one on the left, Slide 1, has the String Stop on the left (in cm and in inches), and the Note (nominal pitch) on the right. The one on the right, Slide 2, has the Diameter on the left (in thou and in mm) and the Pitch Standard on the right. When the Pitch Standard on Slide 2 is against (on the same row as) the Material of the String, and the Note on Slide 1 is against the Diameter on Slide 2, then the String Stop on Slide 1 is against the Tension on the left.
To determine the highest pitch for the string stop of a type of string, one needs to relate Slide 1 with the Highest Pitch column on the far right. To align the rows, one can just look across (perhaps being helped by a horizontal straight edge), or pull out Slide 1 and hold it against the right column, or cut out the Highest Pitch column and attach it to the back of Slide 2 (and for use, turn over Slide 2). When the Set String Stop row in the Highest Pitch column is aligned with the String Stop on Slide 1, then the highest pitch at a'=440 Hz (Note on Slide 1) is aligned with the string material on the Highest Pitch column.
There are a few terms in the two columns concerned with string materials that are not common knowledge. On the column on the left, PVF is polyvinylidene fluoride, a plastic material used for mid-range strings by many lute players. On the column on the right, the strength of gut depends on twist. Low-twist gut has the minimum twist that will give a cylindrical string, giving maximum strength. High twist is the highest twist a normal gut string will take (giving maximum richness of sound) before it starts to take a cork-screw shape. Roped construction results in more richness in sound, and the row assigned to it is for the highest twist. Renaissance iron is the iron that was generally available around 1560. Baroque iron is the iron that became available from around 1580.
Meuler I steel was the string material only made (by a secret process) by Jobst Meuler of Nuremberg from around 1580, and led to the invention of the orpharion and the small English cittern. Meuler II steel was a stronger string material Meuler developed a couple of decades later, which led to the invention of several of the wire-strung instruments described by Praetorius. Meuler's strings ceased to be generally available after about 1620. It was not until piano wire was developed in the 19th century, had a string material became available that again could go to higher pitches than gut. 'Mod' in that column means modern piano wire or spring steel. For further details, see E. Segerman, 'Praetorius's Plucked Instruments and their Strings', FoMRHI Quarterly 92 (July 1998), Comm. 1593, pp.33-7.
When setting up the String Calculator for use, it is suggested that one cuts out the two slides while leaving the top and bottom margins intact. Then glue cardboard or other backing materials (of the same thickness) to both Slides, to the columns on the right and to the column on the left. Then glue the backings on the right and left to a base surface, using the remaining margins on top and bottom for alignment. Finally, cut away those margins around the slides to let them move unhindered.
The theory
The relationship that the main function of the String Calculator depends on is the Mersenne-Taylor formula. In that formula, let us represent the fundamental vibration frequency by f, the string stop by L, the diameter by D, the tension by T and the mass per unit length mL. Then the formula is:
f = (1/2L)sqrt(T/mL). The mass per unit length is the mass per unit volume (the density, represented by ρ) multiplied by the cross-sectional area (represented by A), so mL=ρA. But A=πD2/4. So the formula becomes: f = (1/2L)sqrt(T/ρA) = (1/LD)sqrt(T/ρππ). If we measure the frequency in Hz, the string stop in cm, the diameter in mm, the tension in Kg and the density in gm/cm3, the formula then becomes: f = (5588/LD)sqrt(T/ρ). It is this form of the equation that was used for making the String Calculator except for the highest pitch determination. As with slide rules, distance along the calculator is proportional to the logarithms of the variables, so multiplications are represented by sums of distances.
The stress on the string (represented by S) is the tension divided by the cross-sectional area, so S=T/A. The tensile strength of a material is defined as the stress at breaking (which we can represent by SB). Then the breaking frequency, represented by fB becomes: fB = (1/2L)sqrt(SB/ρ). This demonstrates that the breaking pitch is inversely proportional to the string stop. The highest working pitch tends to be about a semitone lower than the breaking pitch for uniform materials like metals, and a tone below breaking pitch for naturally variable materials like gut. Ultimately, how much below depends on the highest breakage rate the musicians find tolerable, and that historical information has been included here as much as possible. The tensile strengths of metals depend on composition of the alloy and on how hard it is drawn, and the row positions here are for the most common historical examples. If in the playing, the strings are treated rather more roughly, as with the metal tangents of the clavichord, it is appropriate for the highest pitch to be a semitone lower than otherwise.
The previous edition of the String Calculator (published with explanatory material in FoMRHI Quarterly 13 (Oct. 1978), Comm. 162, pp.47-9) also included the lowest pitch for each material. That lowest pitch depends either on deterioration of the resonance and focus of the sound due to inharmonicity, where the harmonics in the tone become very weak and out of tune with the fundamental, or on pitch instability, where the pitch of the note is very sensitive to string streching depending on how hard one plays on the string, and the pressing of the string against a fingerboard. With gut and nylon, inharmonicity is the dominant factor, and with iron and steel, pitch instability is the dominant factor. With the other metals, both factors become intolerable at about the same pitches. Both factors depend on the elastic modulus, tension and string stop, as well as how the string is played, and the relationships are too varied to be expressed simply enough for the String Calculator to provide a reasonably accurate result. A published study of the ranges of gut strings is in E. Segerman, 'Further on the pitch ranges of gut strings', FoMRHI Quarterly 96 (July 1999), Comm. 1657, pp.54-8.
